
Números primos e sua importância para a
Matemática
Na formação do conjunto dos números Naturais existe um tipo de numeral que possui a propriedade de ser divisível somente por um e por ele mesmo, recebendo a denominação de número primo. A descoberta dos números primos é imprescindível na Matemática, pois eles intitulam o princípio central na teoria dos números, consistindo no Teorema Fundamental da Aritmética. Esse Teorema satisfaz uma condição interessante no conjunto dos números naturais, ele afirma que todo número inteiro natural, sendo maior que 1, pode ser escrito como um produto de números primos, enfatizando a hipótese que o número 1 não pode ser considerado primo, pois ele tem apenas um divisor e não pode ser escrito na forma de produto de números primos.
Por meio da fatoração (decomposição dos números em fatores primos) conseguimos representar os números de acordo com o Teorema Fundamental da Aritmética. Vamos observar alguns exemplos onde os numerais serão escritos na forma fatorada.
8 = 2 x 2 x 2
9 = 3 x 3
10 = 2 x 5
27 = 3 x 3 x 3
32 = 2 x 2 x 2 x 2 x 2
50 = 2 x 5 x 5
28 = 2 x 2 x 7
110 = 2 x 5 x 11
1º passo: localizar o primeiro número primo da tabela. (2)
2º passo: marcar todos os múltiplos desse número.
3º passo: localizar o segundo número primo (3) e marcar todos os seus múltiplos.
4º passo: Repetir a operação até o último número.
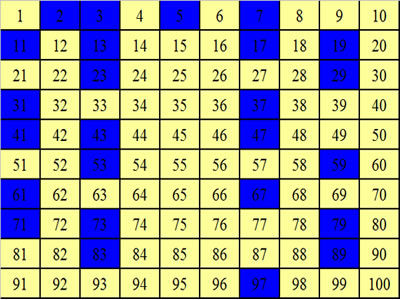
Na tabela dos 100 primeiros números naturais destacamos em azul os números primos, portanto os números primos entre 1 e 100 são: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
FONTE: http://www.brasilescola.com/matematica/numeros-primos.htm
Nenhum comentário:
Postar um comentário