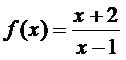N018 - Semana de Reensino II Unidade

Atenção para as NOVAS datas das provas da Semana de Reensino da II Unidade:

Segunda, dia 21:
- Biologia
- Educação para o Trabalho
- Sociologia

Terça, dia 22:
- Química
- História
- Filosofia

Segunda, dia 28:
- Português
- Artes
- Física

Terça, dia 29:
- Matemática
- Educação Física
- Inglês
- Geografia

A025 - Função Inversa

FUNÇÃO INVERSA

Para determinarmos se uma função possui inversa é preciso verificar se ela é bijetora, pois os pares ordenados da função f devem pertencer à função inversa f–1 da seguinte maneira: (x,y) Є f -1 ↔ (y,x) Є f.


Dado os conjuntos A = {-2,-1,0,1,2} e B = {-5,-3,-1,1,3} e a função A→B definida pela fórmula y = 2x – 1, veja o diagrama dessa função abaixo:

Então: f = { (-2,-5); (-1,-3); (0,-1) ; (1,1) ; (2,3)}

Essa função é bijetora, pois cada elemento do domínio está associado a um elemento diferente no conjunto da imagem. Por ser bijetora essa função admite inversa.
A sua função inversa será indicada por f ^-1: B→A definida pela fórmula x = (y-1)/2. Veja o diagrama abaixo:

Então: f ^-1 = {(-5,-2); (-3,-1) ; (-1,0); (1,1) ; (3,2)}

O que é domínio na função f vira imagem na f ^-1 e vice e versa.

Dada uma sentença de uma função y = f(x), para encontrar a sua inversa é preciso seguir alguns passos.

Dada a função y = 3x – 5 determinaremos a sua inversa da seguinte maneira:

1º passo: isolar x.
y = 3x – 5
y + 5 = 3x
x = (y + 5)/3

2º passo: troca-se x por y e y por x, pois é mais usual termos como variável independente a letra x.

y = (x + 5)/3


Portanto, a função f(x) = 3x – 5 terá inversa igual a f ^–1 (x) = (x + 5)/3

Exemplos 1

Dada a função f(x) = x² a sua inversa será:

Isolando x:
y = x²
√y = x

Invertendo x por y e y por x:
y = √x

Portanto, f ^–1(x) = √x


Exemplo 2

Dada a função , a sua inversa será:

Nessa resolução iremos seguir o processo contrário, veja:

Trocando x por y e y por x:



Isolando y:

x (3y – 5) = 2y +3
3xy – 5x = 2y + 3
3xy – 2y = 3 + 5x
y (3x – 2) = 3 + 5x




Portanto, a função inversa da função será f ^-1(x) = .

A024 - Função Composta

FUNÇÃO COMPOSTA

A função composta pode ser entendida pela determinação de uma terceira função C, formada pela junção das funções A e B. Matematicamente falando, temos que f: A → B e g: B → C, denomina a formação da função composta de g com f, h: A → C. Dizemos função g composta com a função f, representada por g o f.

Exemplo 1

Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:

a) g o f

(g o f)(x) = g(f(x))

g(x) = x² + 5
g(4x) = (4x)² + 5
g(4x) = 16x² + 5

(g o f)(x) = g(f(x)) = 16x² + 5



b) f o g

(f o g)(x) = f(g(x))

f(x) = 4x
f(x² + 5) = 4 * (x² + 5)
f(x² + 5) = 4x² + 20

(f o g)(x) = f(g(x)) = 4x² + 20


Exemplo 2

Vamos determinar g(f(x)) e f(g(x)), em relação às funções f(x) = x + 2 e g(x) = 4x² – 1.


(g o f)(x) = g(f(x))

g(x) = 4x² – 1
g(x + 2) = 4 * (x + 2)² – 1
g(x + 2) = 4 * (x + 2) * (x + 2) – 1
g(x + 2) = 4 * (x² + 2x + 2x + 4) – 1
g(x + 2) = 4 * (x² + 4x + 4) – 1
g(x + 2) = 4x² + 16x + 16 – 1
g(x + 2) = 4x² + 16x + 15

(g o f)(x) = g(f(x)) = 4x² + 16x + 15



(f o g)(x) = f(g(x))

f(x) = x + 2
f(4x² – 1) = (4x² – 1) + 2
f(4x² – 1) = 4x² – 1 + 2
f(4x² – 1) = 4x² + 1

(f o g)(x) = f(g(x)) = 4x² + 1

A023 - Domínio de uma Função

As funções devem ser caracterizadas de acordo com algumas condições de existência:

Dois conjuntos: um denominado domínio e outro contradomínio.

Uma expressão y = f(x) associando os valores de x e y, formando pares ordenados pertencentes aos conjuntos domínio e contradomínio.

Através de alguns exemplos demonstraremos como determinar o domínio de uma função, isto é, descobrir quais os números que a função não pode assumir para que a sua condição de existência não seja afetada.

a)

Nesse caso o denominador não pode ser nulo, pois não existe divisão por zero na Matemática.
x – 1 ≠ 0
x ≠ 1
Portanto, D(f) = {x Є R / x ≠ 1} = R – {1}.

b)

Nos números reais, o radicando de uma raiz de índice não pode ser negativo.
4x – 6 ≥ 0
4x 6
x ≥ 6/4
x ≥ 3/2
Portanto, D(f) = {x Є R / x ≥ 3/2}