C002 - Quanto vale um centilhão?

O maior número aceito no sistema de potências sucessivas de dez, é o centilhão, registrado pela primeira vez em 1852. Representa a centésima potência de um milhão, ou o número 1 seguido de 600 zeros (embora apenas utilizado na Grã-Bretanha e na Alemanha).

C001 - O Número Mágico

Você conhece o número mágico?
1089 é conhecido como o número mágico. Veja porque:

Escolha qualquer número de três algarismos distintos: por exemplo, 875.
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297

Agora inverta também esse resultado e faça a soma:
297 + 792 = 1089 (o número mágico).

DV003 - Sobre o número Pi

Vimos essa semana na escola sobre o númerp Pi, uma letra grega, cujo valor aproximado é 3,14. Na verdade, ele é um número irraciona, ou seja, é um decimal infinito e não-periódico.
Aqui abaixo vai uma charge falando sobre quantas casas decimais conhecemos do número Pi!!!!

A016 - Fração Geratriz

Primeiro vamos falar o que é uma dízima periódica.
Dizima periódica é a parte decimal infinita (não tem fim), pois repete igualmente. Por exemplo: 0,22222.... ; 2,5656565656.... ; 0,2555... .

Esses números podem ser escritos em forma de fração, mas apesar de serem números decimais na sua transformação utilizaremos um processo diferente. A fração que dá origem às dízimas periódicas são chamadas de frações geratrizes. Acompanhe o raciocínio:


Exemplo 1:
Vamos transformar 0,2222... em fração. Pra isso chamaremos a dízima de X:

X = 0,2222... (I)

Devemos eliminar as casas decimais. Para isso andaremos com a vírgula para a direita uma casa decimal, pois apenas o 2 que repete. Isso é o mesmo que multiplicar o 0,2222... por 10. Ficando assim:

10 . X = 2,2222... (II)

Temos duas equações (I) e (II). Iremos subtrair as duas:

(II) – (I)


Como X = 0,2222.... , então 0, 2222.... é o mesmo que
Se dividirmos 2 : 9 chegaremos a 0, 2222.... .


Exemplo 2:
Temos a dízima 0, 636363...

X = 0,636363.... (I) andando com a vírgula duas casas para a direita, pois o número que
repete nas casas decimais é o 63.

100 . X = 63,636363.... (II) andar duas casas para a direita é o mesmo que multiplicar
por 100.

Subtraindo as duas equações (II) e (I) encontradas:



Como X = 0,636363... então 0,636363... é o mesmo que

Exemplo 3:
Temos a dízima 2,35555... nessa percebemos que na parte decimal temos apenas o 5.

X = 2,35555...

Como o 3 não faz parte da dízima devemos multiplicar a equação por 10 para que o número 3 passe pro outro lado deixando nas casas decimais apenas a dízima.

10 . X = 23,5555... (I)
Agora, multiplicamos a equação (I) por 10 novamente para que possamos cancelar a parte decimal.

10 . 10 . X = 235,5555...
100 X = 235,5555... (II)

Subtraindo as equações (II) e (I), teremos:



Como X = 2,35555... então 2,35555... é o mesmo que

FONTE: http://www.mundoeducacao.com.br/matematica/transformacao-para-numeros-fracionarios.htm

A015 - Operações com Números Decimais (Parte II)

Multiplicação de número natural por decimal.

A operação de multiplicação e operada com dois fatores e a multiplicação deles resulta em um produto.

6 x 3,25 → são os fatores








Na multiplicação acima:
Quando multiplicamos 5 centésimos por 6 obtivemos 30 centésimos. Deixamos 0 centésimos e transformamos os 30 centésimos em 3 décimos.
Quando multiplicamos 2 décimos por 6 e somamos com 3 obtivemos 15 décimos, deixamos 5 décimos e transformamos os 10 décimos em 1 inteiro.

Para colocarmos a vírgula na casa decimal correta no produto (resultado da multiplicação) devemos olhar o número decimal do fator e contar quantas casas decimais ele tem, no caso do 3,25 tem 2 casas decimais, então devemos contar da direita para a esquerda 2 casas decimais no produto e colocar a vírgula na casa decimal correspondente.


12 x 9,3 → são os fatores

Quando em uma multiplicação o 2º fator for um número natural com mais de um algarismo, devemos multiplicar com o da direita e depois fazer a multiplicação com o da esquerda. O resultados das multiplicações somamos.









Para colocarmos a vírgula na casa decimal correta no produto (resultado da multiplicação) devemos olhar os números decimais dos fatores e contar quantas casas decimais ele tem, no caso do 9,3 tem 1, então andaremos da direita para a esquerda 1 casa decimal e colocaremos a virgula onde paramos.


Multiplicação de decimal por decimal

Para multiplicarmos decimal com decimal resolveremos da mesma forma se fosse multiplicação de número natural com decimal, o que difere é quando formos colocar a vírgula no produto devemos contar as casas decimais dos dois fatores.









Como somando as casas decimais dos dois fatores, teremos 2 casas decimais, assim andaremos 2 casas decimais da direita para a esquerda para colocarmos a vírgula.

FONTE: http://www.mundoeducacao.com.br/matematica/numeros-decimais-multiplicacao.htm



Divisão gerando números decimais.





FONTE: http://www.fadepe.com.br/restrito/conteudo/matematica_num_decimais.doc

A014 - Operações com Números Decimais (Parte I)

Número decimal é aquele número que tem parte inteira e parte decimal, essas são separadas por vírgula.

As quatro operações (adição, subtração, multiplicação e divisão) com os números decimais, para resolver é necessário utilizar algumas regras.


Adição

Para adicionarmos dois ou mais números decimais é preciso colocar vírgula em baixo de vírgula.
Para fazermos qualquer adição, devemos saber que os números somados são chamados de parcelas e o resultado de soma total e que as parcelas tem que ser adicionadas da maior pela menor.

►4,879 + 13,14 → Parcelas


Na soma de 4 centésimos com 7 centésimos é igual a 11 centésimos, assim fica um e “vai um”.

► 2 + 1, 751



►0,3 + 1

Subtração

Para subtrairmos dois números decimais, devemos da mesma forma que na adição colocar vírgula de baixo de vírgula de vírgula.
Sendo que o diminuendo deve ser sempre maior que o subtraendo e o resultado recebem o nome de resto ou diferença.

• 7,37 – 2,8 → minuendo e subtraendo nessa mesma ordem.


Para subtrair 8 décimos, transformamos 1 inteiro em 10 décimos, ficando com 13 décimos no minuendo. Assim fazemos:
13 – 8 = 5
6 – 2 = 4

► 0,25 - 0,18

Pra subtrair 8, transformamos 1 décimo em 10 centésimos, ficando com 15 o minuendo. Assim fazemos:
15 – 8 = 7
1 – 1 = 0


FONTE: http://www.mundoeducacao.com.br/matematica/numeros-decimais-adicao-subtracao.htm

A013 - Multiplicação e Divisão de Frações

Multiplicação de Frações

Os exemplos a seguir demonstrarão passo a passo o andamento de uma multiplicação envolvendo números racionais na forma fracionária.

Exemplos:

Caso seja necessário, os produtos apresentados e que constituem frações, podem ser escritos de forma mais simples, isto é, na forma de fração irredutível. Para tal procedimento utilizamos a simplificação de frações, que é feita encontrando o maior divisor comum ao numerador e ao denominador. Veja exemplos de simplificação:




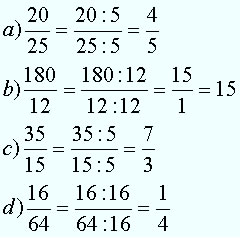
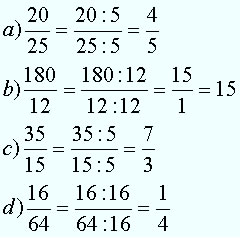
FONTE: http://www.brasilescola.com/matematica/multiplicacao-com-fracao.htm



Divisão de Frações

Pra realizarmos uma divisão entre frações, operamos da seguinte forma: repetimos a primeira fração e multiplicamos pelo inverso da segunda fração.

Exemplo:


Ao final da operação, caso seja necessário, simplicamos o resultado até obtermos a fração irredutível.

A012 - Adição de Frações

Quando os denominadores forem iguais devemos somar ou diminuir as partes consideradas do inteiro (numeradores) e conservar as partes que o inteiro foi dividido (denominadores).

1/5 + 2/5 = 3/5, pois somamos os numeradores 1 + 2 e conservamos o denominador 5.

3/4 + 2/4 = 5/4, pois somamos os numeradores 3 + 2 e conservamos o denominador 4.

2/5 – 1/5 = 1/5, pois subtraímos os numeradores 2 -1 e conservamos o denominador 5.

Quando os denominadores forem diferentes é preciso torná-los iguais antes de resolver a operação de adição ou subtração, utilizando as técnicas que a redução de uma fração ao mesmo denominador oferece.

Para resolver 1/5 + 2/10 é preciso que encontremos o MMC de 5 e 10 (os denominadores diferentes das frações) que será o próprio 10. Assim, o denominador comum das frações 1/5 e 2/10 será 10.

Depois de encontrar o “novo denominador” temos que dividí-lo pelo “antigo” e multiplicar o resultado pelo numerador, devemos fazer sempre esse processo, pois se mudamos o denominador temos que encontrar um numerador proporcional.

Encontrando assim as respectivas frações equivalentes 2/10 e 2/10. Com essas frações efetuamos a soma:


FONTE 1: http://www.brasilescola.com/matematica/adicao-subtracao-fracao.htm

FONTE 2: http://www.brasilescola.com/matematica/reducao-fracao-ao-mesmo-denominador.htm

A011 - Simplificação de Frações

A simplificação de fração é um método prático de encontrar frações equivalentes. Ao simplificarmos uma fração o seu valor numérico não é alterado, pois a simplificação consiste em dividir tanto o numerador como o denominador pelo mesmo número (desde que seja diferente de zero).

Quando não existir nenhum número que divida tanto o numerador como o denominador, ou seja, se não tiver como simplificar a fração dada, essa será considerada uma fração irredutível. Ao simplificarmos uma fração temos como objetivo torná-la irredutível.

Dada a fração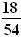 , simplificamos pelo menor divisor comum entre o numerador e o denominador.



FONTE: http://www.brasilescola.com/matematica/simplificacao-fracao.htm