E001 - Introdução a Conjuntos (Caderno)

O exercício abaixo foi passado na primeira semana de aulas e possui três questões envolvendo operações com conjuntos e subconjuntos. Abaixo, a resolução de cada questão.


1) Escreva quais são os elementos que representam cada conjunto:

Resposta: Esse conjunto é formado pelos números naturais entre 1 e 8. O sinal de "menor ou igual que" indica que também contamos o 1 e o 8. Então, esse conjunto é {1, 2, 3, 4, 5, 6, 7, 8}.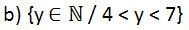

Resposta: Esse conjunto é formado pelos números naturais entre 4 e 7. O sinal de "menor que" indica que não contamos o 4 nem o 7. Então, esse conjunto é {5, 6}.

c) (z / z é vogal}
Resposta: Esse conjunto é formado pelas vogais, logo {a, e, i, o, u}.

d) {a / a é consoante depois de z}
Resposta: Como não existem consoantes depois de "z", esse é um conjunto vazio, logo { }.

e) {m / m é cor da bandeira do Brasil}
Resposta: com as quatro cores da nossa bandeira formamos esse conjunto, {verde, amarelo, azul, branco}.


2) Dados os conjuntos A = {0, 1, 2, 3, 4} e B = {1, 3, 5, 7}, determine:

a) A U B
Resposta: Para formar a união dos conjuntos A e B, basta juntar todos os elementos sem repetí-los = { 0, 1, 2, 3, 4, 5, 7}.

Resposta: Para obter a intersecção dos conjuntos A e B, basta escrever os elementos que se repetem nos dois conjuntos = {1, 3}.

c) A - B
Resposta: Pegamos os elementos de A e retiramos dele os que aparecem em B. Nesse caso, sobram apenas = {0, 2, 4}.

d) B - A
Resposta: Pegamos os elementos de B e retiramos dele os que aparecem em A. Nesse caso, sobram apenas = {5, 7}.

e) representação em forma de diagrama








3) Dê os subconjuntos dos conjuntos a seguir:



Resposta: Primeiro temos que descobrir quais elementos fazem parte desse conjunto. Os números naturais menores que 3 são 0, 1 e 2. Com esses três elementos vamos formar todos os subconjuntos possíveis. Então = {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2} e { }.

b) S = { s / s representa as três primeiras consoantes}
Resposta: Primeiro temos que descobrir quais elementos fazem parte desse conjunto. As três primeiras consoantes são b, c, d. Com esses três elementos vamos formar todos os subconjuntos possíveis. Então = {b}, {c}, {d}, {b, c}, {b, d}, {c, d}, {b, d, d} e { }.

c) T = {5, 8}
Resposta: Com esses dois elementos vamos formar todos os subconjuntos possíveis. Então = {5}, {8}, {5, 8} e { }.