Dois conjuntos: um denominado domínio e outro contradomínio.
Através de alguns exemplos demonstraremos como determinar o domínio de uma função, isto é, descobrir quais os números que a função não pode assumir para que a sua condição de existência não seja afetada.
a)
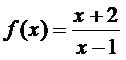
Nesse caso o denominador não pode ser nulo, pois não existe divisão por zero na Matemática.
x – 1 ≠ 0
x ≠ 1
Portanto, D(f) = {x Є R / x ≠ 1} = R – {1}.
b)
Nos números reais, o radicando de uma raiz de índice não pode ser negativo.
4x – 6 ≥ 0
4x 6
x ≥ 6/4
x ≥ 3/2
Portanto, D(f) = {x Є R / x ≥ 3/2}
Nenhum comentário:
Postar um comentário