Inequações-Produto

EXEMPLO 1:

Resolver uma inequação produto consiste em encontrar os valores de x que satisfazem a condição estabelecida pela inequação. Para isso utilizamos o estudo do sinal de uma função. Observe a resolução da seguinte equação produto: (2x + 6)*( – 3x + 12) > 0.

Vamos estabelecer as seguintes funções: y₁ = 2x + 6 e y₂ = – 3x + 12.

Determinando a raiz da função (y = 0) e a posição da reta (a > 0 crescente e a <>1 = 2x + 6
2x + 6 = 0
2x = – 6
x = –3

y₂ = – 3x + 12
–3x + 12 = 0
–3x = –12
x = 4

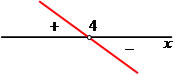
Verificando o sinal da inequação produto (2x + 6)*(– 3x + 12) > 0. Observe que a inequação produto exige a seguinte condição: os possíveis valores devem ser maiores que zero, isto é, positivo.

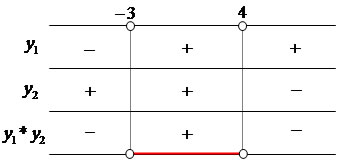
Através do esquema que demonstra os sinais da inequação produto y1*y2, podemos chegar à seguinte conclusão quanto aos valores de x:

S = { x e R / - 3 < x < 4}

EXEMPLO 2:

Ache o conjunto solução da equação produto abaixo:
(-3x + 6) (5x -7) < 0

1) -3x + 6< 0
- 3x < -6 x(-1)
3x > 6
x > 6/3
x > 2








2) 5x – 7 = 0
5x = 7
x = 7/5





Fazendo o jogo de sinal com o estudo de sinal em cada coluna formada por uma função:


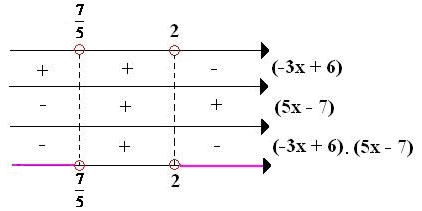
Como a inequação quer valores que sejam menores que 0 escrevemos que o conjunto solução da inequação será:

S = { x e R / x <> 2}



EXEMPLO 3:

x . (x – 1) (-x + 2) ≤ 0

x = 0


x – 1 = 0
x = 1


-x + 2 = 0
-x = -2
x = 2


Fazendo o jogo de sinal com o estudo de sinal em cada coluna formada por uma função:


Como a inequação quer valores que sejam menores ou iguais a 0 escrevemos que o conjunto solução da inequação
x . (x – 1) (-x + 2) ≤ 0, será:

S = {x Є R / 0 ≤ x ≤ 1 ou x ≥ 2}.


FONTE 1: http://www.brasilescola.com/matematica/inequacao-produto-1.htm
FONTE 2: http://www.brasilescola.com/matematica/inequacao-produto-e-quociente.htm
FONTE 3: http://educacao.uol.com.br/matematica/inequacao-produto-e-inequacao-quociente.jhtm