EXEMPLO 1:
Na resolução da inequação quociente utilizamos os mesmos recursos da inequação produto, o que difere é que, ao calcularmos a função do denominador, precisamos adotar valores maiores ou menores que zero e nunca igual a zero. Observe a resolução da seguinte inequação quociente:

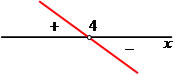
Resolver as funções y1 = x + 1 e y2 = 2x – 1, determinando a raiz da função (y = 0) e a posição da reta (a > 0 crescente e a <>1 = x + 1
x + 1 = 0
x = –1

y2 = 2x – 1
2x – 1 = 0
2x = 1
x = 1/2


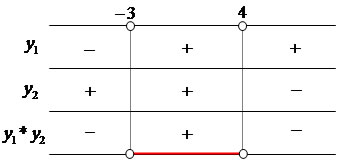
Com base no jogo de sinal concluímos que x assume os seguintes valores na inequação quociente:
S = { x e R / -1 <>
EXEMPLO 2:

 |
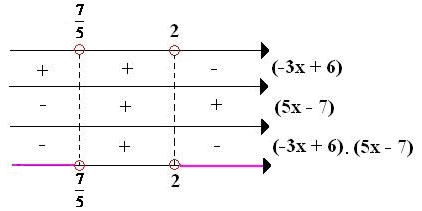
Sem precisar traçar os gráficos, podemos esboçá-los, conhecendo as raízes e o crescimento de cada uma, olhando para o sinal do coeficiente de x.
A) coeficiente de x = -1 < raiz =" 2">
 |
B) coeficiente de x = 2 > 0
Função crescente
Raiz =

 |
Atenção: Não é o sinal da raiz que determina o crescimento ou decrescimento da função, mas o sinal do coeficiente de x. Esse é um erro bem comum! Cuidado!
Estudados os sinais, vamos ao quadro de sinais:
 |
É importante notar: apesar de querermos os valores de x que tornam o quociente negativo ou nulo, não devemos incluir nunca na solução o valor de x que anula o denomidador da fração (a raiz da expressão do denominador), pois não existe fração com denominador nulo. Esse é outro erro comum!
Logo, a solução é

FONTE 1: http://www.brasilescola.com/matematica/inequacao-produto-e-quociente.htm
FONTE 2: http://educacao.uol.com.br/matematica/inequacao-produto-e-inequacao-quociente.jhtm